Table of Contents
Errors in pharmaceutical analysis
During an analysis, the results are expected to be highly accurate and precise. However, it is not happening in all cases. The high degree of precision obtained in the analysis may not necessarily be accurate. There may be reproducible results that deviate from the accuracy. Thus, a constant error may result in reproducible results with good precision due to factors such as defective equipment and methods. Errors happened in the pharmaceutical analysis due to various factors.
These errors may be predictable or unpredictable. Depending on the nature and source, errors have been classified and discussed below.
Two major categories of errors are known as absolute errors and relative errors. The difference between the experimental mean and a true value is known as ‘absolute error’.
Sometimes the term ‘relative error’ is used in the analysis. The relative error is the value found by dividing the absolute error by the true value. Thus,
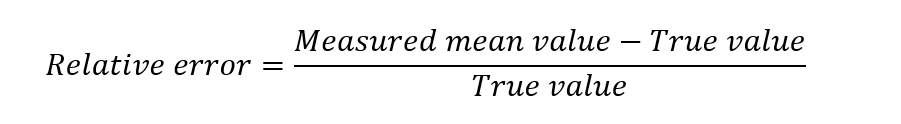
The relative error is generally expressed as a percent, that is, by multiplying the relative error by 100 or by expressing it as parts per thousand by multiplying the relative error by 1000.
Sources and Types of Errors
In pharmaceutical analysis, it is generally accepted that the results of the analysis are subject to errors. The variations or differences in the results are caused by errors from various sources and these errors are of different natures. Depending on the nature of errors that affects the accuracy or precision of a measured quantity, they are classified into two main classes:
- Determinate Errors
- Indeterminate Errors
1. Determinate Errors:
These are ascertainable errors that can be either avoided or corrected. The error may be constant as in the case of weighing with uncalibrated weights or in measuring a volume using a burette or pipette. Such measurable determinate errors are categorized as systematic errors. The determinate errors arise due to,
(a) Instrumental errors: These errors are caused by faulty equipment or low-quality equipment which do not perform well.
(b) Personal errors: These errors occur by persons who are handling the method of analysis. The error may be resulted due to carelessness or ignorance and even from unskilled persons. This error is also called operative error.
(c) Chemical errors: These errors are resulted from using chemicals and reagents with impurities or contaminants which may interfere with the reactions, thus affecting the results.
(d) Errors in the methodology: This is a most serious error in the analysis as the error arises due to faulty method, e.g. co-precipitation of impurities, slight solubility of precipitate, incomplete reactions, etc. Errors in this category are usually detectable and can be eliminated to a large extent.
2. Indeterminate Errors:
Indeterminate errors are often called accidental or random errors. They are revealed by small differences in a series of measurements made by the same analyst under identical conditions. They cannot be predicted and hence cannot be eliminated. Such accidental errors will follow a random distribution pattern and the mathematical laws of probability can be applied to get a net conclusion regarding the results.
The random distribution of indeterminate errors of various magnitudes is shown in a graph.
The magnitude of error (abscissa) and the frequency of deviation (ordinate) have the shape of a normal frequency distribution curve or probability curve. This graph is also called a ‘Curve of error’. From the graph, it will be seen that:
- Very large errors are unlikely to occur.
- Smaller errors occur with greater frequency than large errors, and
- The errors on the positive and negative sides occur with equal probability.
Make sure you also check our other amazing Article on: Primary And Secondary Standards
