Sorensen’s Ph Scale can explain, the hydrogen ion concentration in pure water at room temperature is about 1.0 × 10−7 M. Since every water solution contains hydrogen ions, their concentration is one of the most important parameters describing solution properties. The pH scale was defined because the enormous range of hydrogen ion concentrations found in aqueous solutions makes using H+ molarity awkward. For example, in a typical acid-base titration, [H+ ] may vary from about 0.01 M to 0.0000000000001 M. Such numbers are inconvenient to use but it is easier to write as “the pH varies from 2 to 13”.
To simplify things Danish biochemist Soren Sorensen in 1909 developed the pH scale and introduced pH definition as minus (−) logarithm of [H + ] to the base 10. A pH of 7 is considered “neutral” because the concentration of hydrogen ions is exactly equal to the concentration of hydroxide (OH− ) ions produced by dissociation of the water. Increasing the concentration of hydrogen ions above 1.0 × 10−7 M produces a solution with a pH of less than 7, and the solution is considered as “acidic”. On other hand decreasing the concentration of hydrogen ions below 1.0 × 10−7 M produces a solution with a pH above 7, and the solution is considered “alkaline” or “basic”.
The pH is an indication of the degree of acidity or basicity (alkalinity) relative to the ionization of water. The term pH is an abbreviation for “pondus hydro genii” (translated as potential hydrogen) meaning hydrogen power, as acidity is caused by a predominance of hydrogen ions. Initially, pH was written as PH. According to the Compact Oxford English Dictionary, the modern notation “PH” was first adopted in 1920 by W. M. Clark. The letter “p” in the term “pH” stands for the German word “potenz” (power), so pH is an abbreviation for “power of hydrogen”. In simple terms, pH is a logarithmic measure of hydrogen ion concentration.
pH = − log [H+ ]…………(1)
where the log is a base −10 logarithm and [H+ ] is the concentration of hydrogen ions in moles per liter of solution.
With the progress and development of the theory of chemical reactions, the definition of pH was reexamined. As the role and behavior of electrical charge in chemical reactions became better understood, the definition of pH was changed to consider the active hydrogen ion concentration. Debye, Huckle, and Lowry described a more detailed and theoretically more complete definition of pH.
pH = − log aH+……..(2)
where aH+ is the hydrogen ion activity meaning the effective concentration of hydrogen ion.
There is a difference between concentration and activity for acids, but the same holds true for bases.
- In dilute solutions (0.001 molars = 1mM) all anions and all cations are so far apart that they are capable to produce the maximum of the chemical energy, i.e. [H+ ] = aH+.
- At higher acid or base concentrations, the physical spacing between cations and anions decreases, such that they begin to obstruct each other, and shield each other’s charge. Therefore, the mobility of any ion is impaired by interactions with other ions and their associated electrical fields. These local electric field interactions affect the extent to which the ions can participate in chemical reactions, and give an apparent concentration that is always smaller than the real concentration. In this case, the ion activity is “slowed down”; specifically, [H+ ] >aH+.
- The difference between ion activity and concentration increases with the acid concentration. Therefore, for acid concentrations greater than 1mM it is generally advisable to use activities instead of concentrations to accurately predict pH.
The pOH
Not only H+ ions are present in every water solution but OH− ions are also always present, and their concentration can change in a very wide range. Thus, it is convenient to use a similar definition to describe [OH− ].
pOH = − log [OH−]……….(3)
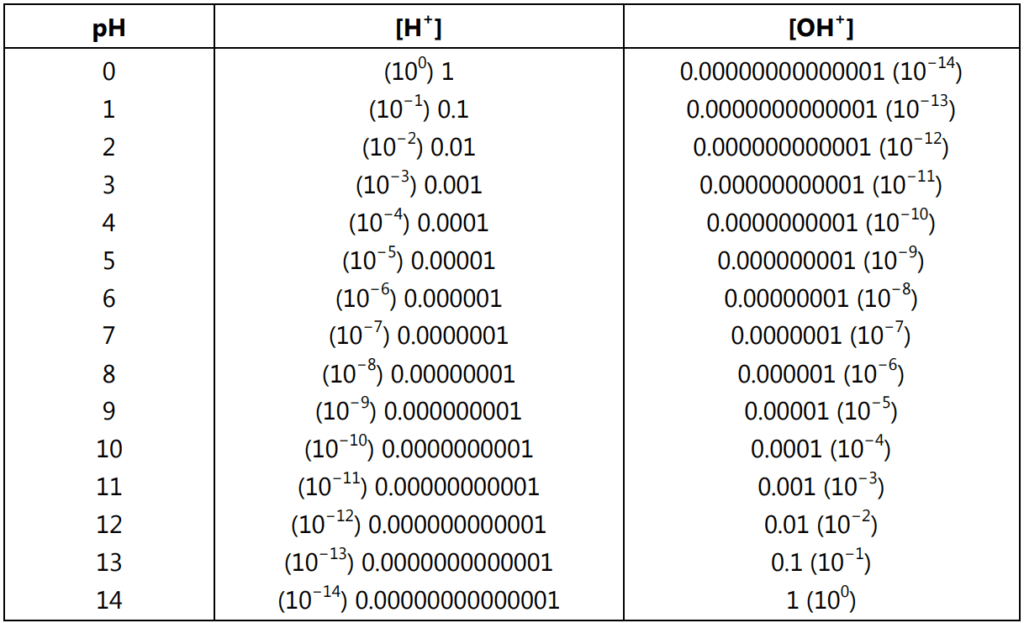
In real solutions, ion activities rather than concentrations should be used for calculations. The definition of pH uses the minus logarithm of activity and not the minus logarithm of concentration. In diluted solutions activity, for all practical purposes is identical to concentration. It means when the concentration goes higher activity starts first to be lower than the concentration and then once the concentration rises it becomes higher than the concentration. If the concentration of charged ions present in the solution is below 0.001M then don’t be concerned about activities and use classic pH definition. The relationship between pH, [H+ ] and [OH+ ] in moles/L at 25 °C is given in Table 1.1.
The presence of hydrogen ions in solutions allows us to measure the pH of a solution. The quantity of hydrogen ions (cations) or hydroxyl ions (anions) in a solution determines whether the solution is acidic or alkaline. The concentrations of hydrogen and hydroxyl ions in pure, acidic, and alkaline aqueous solutions are used to find the following ionic concentrations:
Pure water:
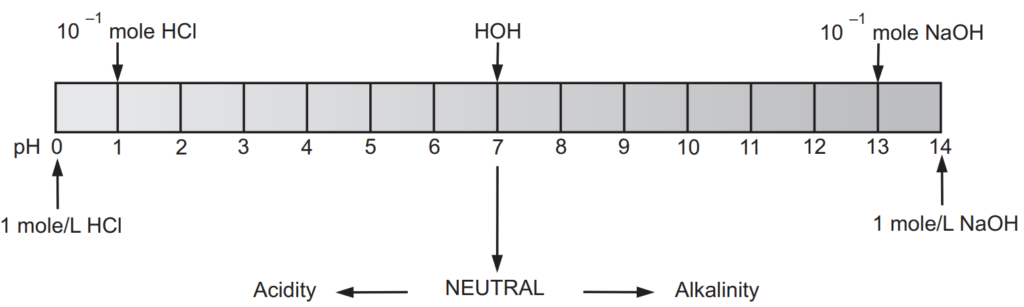
[H+ ] = 1 × 10−7 moles/L and [OH− ] = 1 × 10−7 moles/L
Acidic water (1 molar aqueous HCl):
[H+ ] = 1 × 10° moles/L and [OH− ] = 1 × 10−14 moles/L
Alkaline water (1 molar aqueous NaOH):
[H+ ] = 1 × 10−14 moles/L and [OH− ] = 1 × 10° moles/L
The concentration of H+ ions has major effects on most of the chemical reactions. Depending on concentration hydrogen peroxide can behave as an oxidizing or reducing agent, pepsin an enzyme used for digestion works best in strongly acidic conditions (which becomes inactive in neutral solutions) and tea changes its color on the addition of a slice of lemon. Therefore, the acidity of the solution is of such importance that it was convenient to create a pH scale for its measurements based upon the use of Sorensen’s pH definition.
In aqueous solutions, the reversible reaction between hydrogen ions, hydroxyl ions, and water molecules, namely H+ + OH−àH2O. It leads to the following equation:
[H+ ] × [OH−] = 10−14……(4)
The pH scale shown in Fig. 1.1 indicates both [H+ ] and [OH− ] through this relationship. The mid-point of 7 on the pH scale indicates ionic neutrality of the solution, when [H+ ] = [OH− ]. The range of acid pH values extends from 0 to 7, while that of alkaline pH values from 7 to 14. Fig. 1.2 illustrates these ranges and provides some examples of common acidic and alkaline solutions.
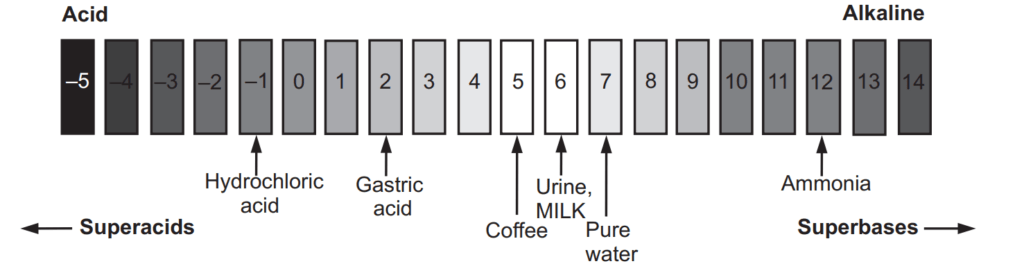
On the pH scale, pure water has pH 7. Since air always contains small amounts of carbon dioxide, it dissolves in water to make it slightly acidic with a pH of about 5.7. The lower the pH, the more acidic solution, and solutions with pH above 7 are basic, and hence higher the pH the more basic solution is. As the pH scale is logarithmic, it does not start at zero. The most acidic of liquids can have a pH as low as −5. The most alkaline solution has a pH of 14. Measurement of extremely low pH values has various complications.
There are two important things about the pH scale.
- As the pH scale is logarithmic, a 1 unit pH change means a tenfold change in the H+ ion concentration.
- The only solution with pH = 7 is strictly neutral and all solutions with pH in the range 4 to 10 have real concentrations of H+ and OH− lower than 10−4 M which can be easily disturbed with small additions of acid and base.
The pH scale described earlier is sometimes called the “concentration pH scale” because it considers H+ ion concentration. The other one is called the “thermodynamic pH scale” which considers the H+ activity rather than the H+ ion concentration. Using pH electrodes we measure just activity and not the concentration in the solution and thus it is a thermodynamic pH scale. It describes real solutions but not the concentration. The concentration pH scale is defined for pure substance and not for water solution whereas the thermodynamic pH scale can be defined not only for water solutions but also for some other solvents, like methanol, ammonia, acetic acid, etc. The range of pH for such solvents depends on their ion product, for example, pH for acetic acid ranges from 0 to 15.2 while pH for methanol ranges from 0 to 16.7.
Make sure you also check our other amazing Article on : Pharmaceutical Pellets