Raoult’s law states that a solvent’s partial vapour pressure in a solution or mixture is equal to the vapour pressure of a pure solvent multiplied by its mole fraction in the solution.
In an ideal solution, volume changes are negligible. Dilute solutions show colligative properties. These properties are the factors that determine how the properties of a bulk solution change depending upon the concentration of the solute in it. Colligative properties are properties of a solution that depend mainly on the relative numbers of particles of solvent and solute molecules and not on the chemical properties of the molecules themselves. These can almost be referred to as statistical properties because they can be understood solely based on the relative number of different particles in a solution. There are four types of colligative properties namely:
- Lowering of vapour pressure.
- Elevation of boiling point.
- Depression of freezing point.
- Osmotic pressure…
The colligative properties of non-electrolyte solutions are regular. The values of colligative properties are approximately equal for an equimolar concentration of drugs. It is possible to determine the number of solute particles present in the solution by measuring these properties and comparing them with the corresponding properties of the pure solvent. If the mass of solute present is known, the number average molecular weight can be calculated by dividing the mass of solute by a number of particles present to obtain the average mass of particles. Osmotic pressure is the most important colligative property since it is related to the physiological compatibility of parenteral, ophthalmic and nasal solutions. It is difficult and inconvenient to measure osmotic pressure and therefore other colligative properties are determined and related to osmotic pressure.
In the following section equations for colligative properties of the ideal solution are derived and are validated for this type of solution. These equations can be applied to real solutions with respect to the limit of small concentrations. While using these equations for real (non-ideal) solutions it requires correction to be made to these ideal equations because in real solutions there exist intermolecular interactions.
Table of Contents
Lowering of Vapour Pressure
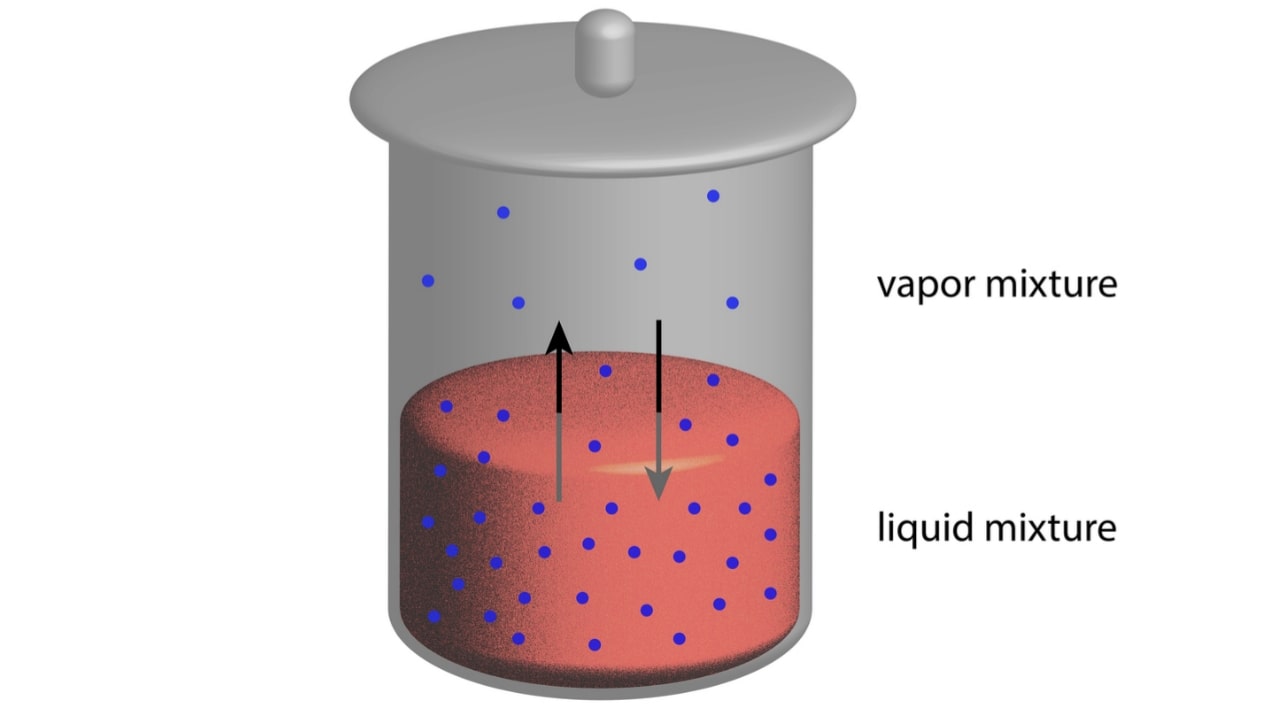
Lowering of vapour pressure is the simplest of the colligative properties and easiest to understand based on a physical model. The pressure brought by a vapour in equilibrium with its liquid at a constant temperature is known as vapour pressure. It increases with temperature. The vapour pressure of the solvent is due to its escaping tendency. The temperature at which the vapour pressure of the liquid is equal to the atmospheric pressure is called a normal boiling point. The vapour pressure of pure liquid solvent depends upon the rate of escape of molecule from the surface known as escaping tendency. Solvents with greater escaping tendencies have a greater vapour pressure.
The added solute is generally non-volatile which does not contribute directly to the vapour pressure of the solution. The solute interferes and prevents solvent molecules from escaping into the atmosphere. Therefore, the vapour pressure of the solution is lower than that of the pure solvent. The lowering of vapour pressure is proportional to the number of solute particles or ions. The effect of non-volatile solute on the vapour pressure may be determined in dilute solutions by applying Raoult’s law. It states that in an ideal solution the partial vapour pressure of each volatile constituent is equal to the vapour pressures of pure constituent at that temperature multiplied by its mole fraction in the solution. In equation form for two volatile constituents A and B, it can be expressed as
PA = PA0XA ———————————(1)
PB = PB0XB ———————————(2)
where PA and PB are partial vapour pressures, PA° and PB° are vapour pressures of pure constituents and XA and XB are mole fractions of the constituent A and B, respectively. The total vapour pressure of the solution is the sum of the partial vapour pressure of each volatile constituent. Therefore,
P = PA + PB———————————-(3)
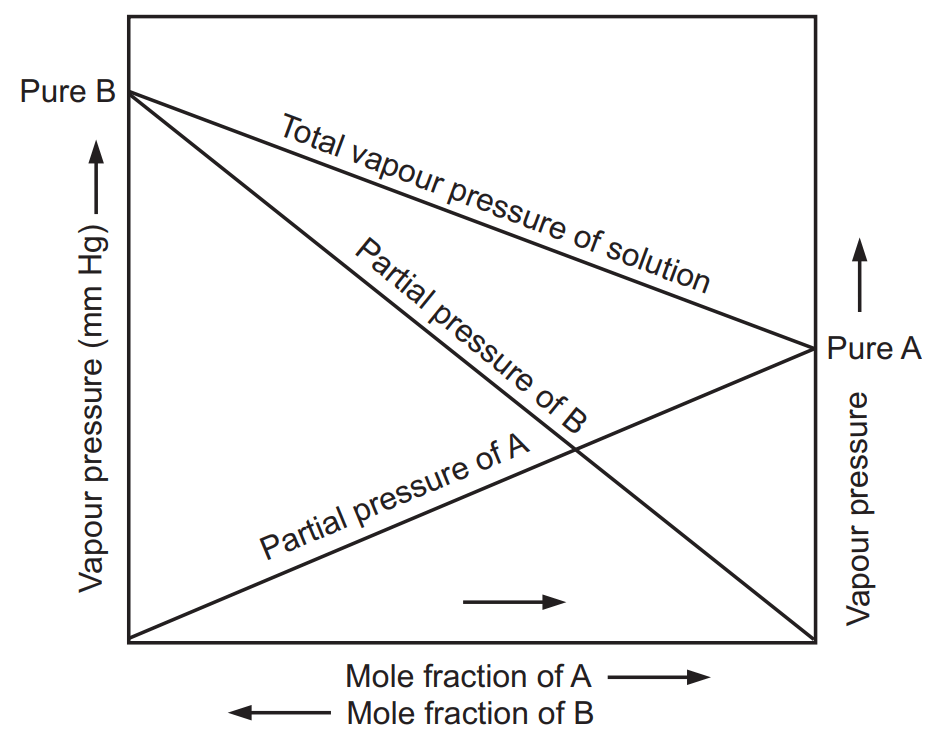
Vapour Pressure of their Solution at Different Mole Fraction
The partial vapour pressure of A and B and the total vapour pressure of the solution is shown in Fig. 1.1. There are two ways to explain Raoult’s law. First, the simple visual way and the second one is a more sophisticated way based upon entropy. To describe using a simple way, consider that equilibrium is set-up where the number of molecules of solvent breaking and escaping away from the surface and some of them are sticking on to the surface again as shown in Fig. 1.2. An added solute molecule to the solvent replaces some of the solvent molecules present at the surface causing a reduction in surface area.
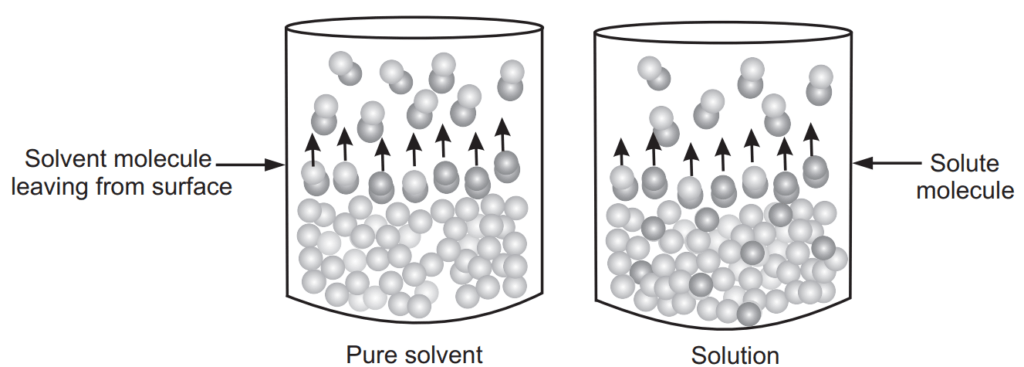
A certain fraction of the solvent molecules have enough energy to escape from the surface. If these molecules are decreased as added solute replaces some of them causing a reduction in the number of molecules escaping from the surface. The net result of this reduction in number is that the vapour pressure of the solvent is reduced. The composition of the solution in terms of mole fraction can be expressed as
XA + XB = 1———————————-(4)
therefore, XA = 1 – XB—————————————-(5)
Substituting equation (5) ) in equation (1) gives
PA = PA° (1 – XB)—————————————(6)
Simplifying equation (6) we get
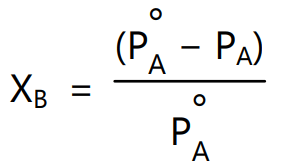
Substituting terms for mole fraction in equation (7) gives
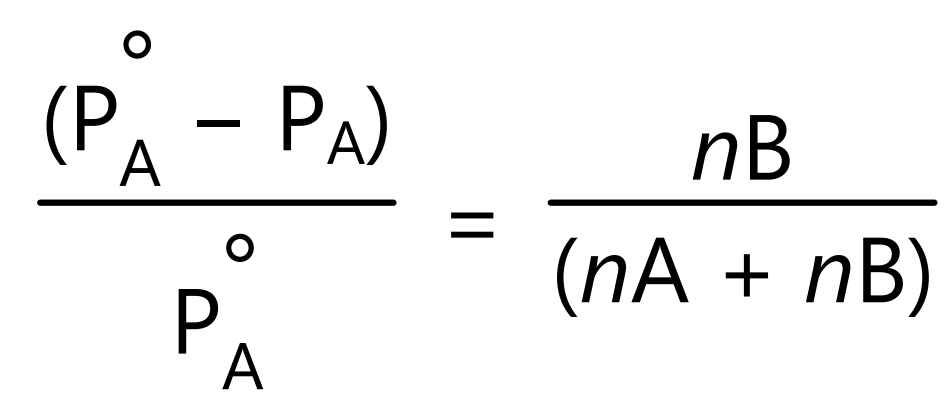
where nA and nB are the numbers of moles of solute and solvent. Above equations (7) and (8) shows that relative lowering of the vapour pressure of the solution is equal to the mole fraction of the solute. The mole fraction and vapour pressure in equation (7) and (8) has no units because these are relative expressions. Hence any units consistent with the system can be used.
Deviations from Raoult’s Law:
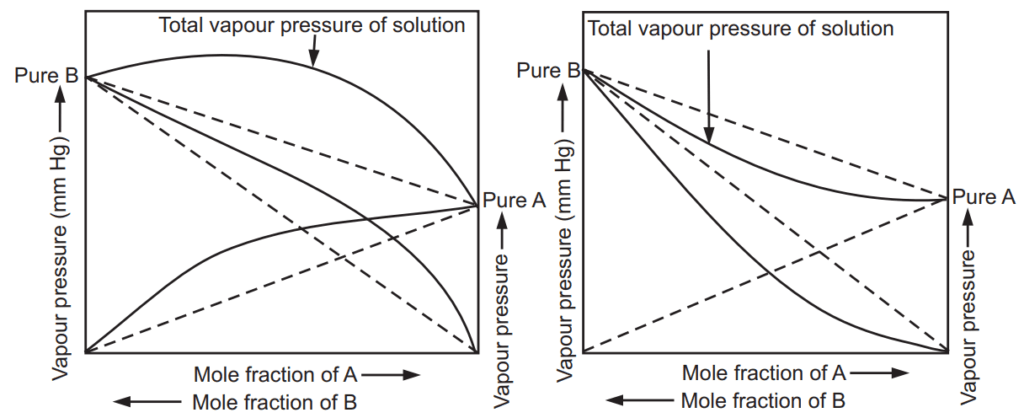
In real solutions, there is no complete uniformity of intermolecular attractive forces. There are many such liquid pairs that show greater cohesive forces than the attractive forces and greater attractive forces than the cohesive forces. It can be observed even when liquids are completely miscible in all proportions. Such mixtures of liquid pairs are real or non-ideal solutions. They do not adhere to Raoult’s law over the entire range of concentrations and are represented as deviations. This behaviour shown by liquid mixtures is called positive deviation, Fig. 1.3 (a) and negative deviation, Fig. 1.3 (b).
Limitations of Raoult’s Law:
Raoult’s law work only for ideal solutions over an entire range of concentrations. An ideal solution obeys Raoult’s law. While applying this law to real solutions has the following limitations.
Real Solutions:
In real solutions, the concentration of solute is high and thus intermolecular forces between solute-solute and solute-solvent are predominant that slowing down the escaping of solvent molecules from the surface. This causes deviation from Raoult’s law because it is applicable only to dilute solutions where the forces between solute and solvent are exactly the same as those between solvent-solvent molecules.
Nature of the Solute:
Raoult’s law is applicable only for solutes which are non-volatile in nature. Volatile solutes can contribute to vapour pressure above the solution which may cause the deviation from Raoult’s law. Raoult’s law does not apply if the added solute associates or dissociates in the solvent. If association takes place the number of particles or molecules decreases causing the reduction in the lowering of vapour pressure. On the contrary, if solute gets dissociated more number of particles or ions are formed. For example, when 1 mole of solid sodium chloride is added to water it dissociates to produce two moles of ions like Na+ and Cl–
Na+ Cl–(solid) → Na+ (aq) + Cl– (aq)
If 0.1 mole of sodium chloride is added to water its dissociation takes place to form 0.2 moles of particles in solution. Thus, it increases the lowering of the vapour pressure of the solution.
Make sure you also check our other amazing Article on : Proof Spirit